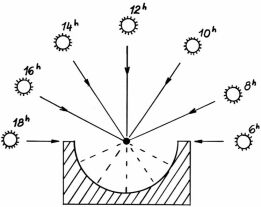
Ke snazšímu porozumění činnosti slunečních hodin si připomeneme základní poznatky z astronomie a zeměpisu. Země vykonává několik pohybů, z nichž jsou nejpatrnější ve svých důsledcích dva - viz obr.
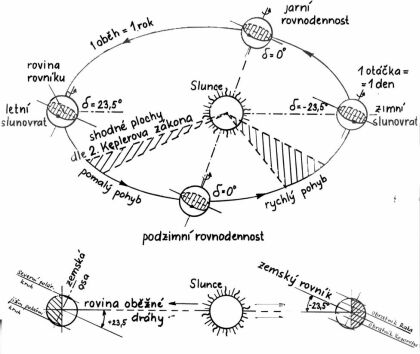
Země se otáčí kolem své osy jednou za den a jednou za rok oběhne Slunce. Rotace Země kolem své osy je příčinou zdánlivého oběhu Slunce od východu k západu. Roční oběh kolem Slunce má za následek, že zdánlivá denní dráha Slunce po obloze se během roku mění.
Dráha Země není kruhová, ale eliptická. Slunce leží v jednom jejím ohnisku. Vzdálenost Země od slunce se v průběhu roku mění, je-li mu nejblíže, je v přísluní nebo-li perihelu, je-li nejdále, mluvíme o odsluní nebo afelu.
V důsledku 2. Keplerova zákona je pohyb Země kolem Slunce nerovnoměrný. Nejrychleji se Slunce pohybuje v perihelu, nejpomaleji v afelu. Časový interval od jarní (21. 3.) do podzimní rovnodennosti (23. 9.) trvá 186 dní, kdežto druhá polovina roku 179 dní (rozdíl celého týdne). Navíc zemská osa není k rovině zemské dráhy kolmá, ale je od kolmice odkloněna přibližně o 23,5°. Obě uvedené skutečnosti mají za následek, že zdánlivý pohyb Slunce po obloze je nerovnoměrný a hodiny na slunečních hodinách mění v průběhu roku svoji délku.
Pravý sluneční čas neplyne rovnoměrně. Mechanické (krystalové) hodiny užívají čas rovnoměrný. Proto se zavádí tzv. střední sluneční čas. Ten odpovídá stejně dlouhým hodinám. Při porovnání údaje času slunečních hodin s mechanickými (krystalovými) pak dochází k odchylce, která často vede k názoru o nesprávnosti údaje slunečních hodin. Rozdíl obou časů však i u přesně zhotovených ("přesně jdoucích") slunečních hodin vyplývá z odlišného stanovení obou typů času a v důsledku platnosti fyzikálních principů.
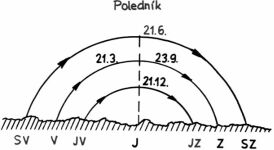
Pravé sluneční poledne nastává v okamžiku, kdy je Slunce nejvýše na své zdánlivé dráze (vrcholí) a svou polohou na obloze ukazuje přesný jih. Pokud jsou sluneční hodiny navrženy pro časový údaj pravého/slunečního místního času (PMČ) leží stín v tomto okamžiku na svislici. Na tomto jednoznačném okamžiku lze nejlépe objasnit rozdílnost obou časových údajů.
V důsledku eliptické dráhy Země okolo Slunce a dalších zákonů (viz výše) je zdánlivý pohyb Slunce po obloze nerovnoměrný a hodiny na slunečních hodinách mění v průběhu roku svoji délku.
Podle tzv. časové rovnice okamžik slunečního poledne v místě středoevropského poledníku (15°) kolísá během roku od časového znamení v rozhlase pro poledne až zhruba o 16 minut.
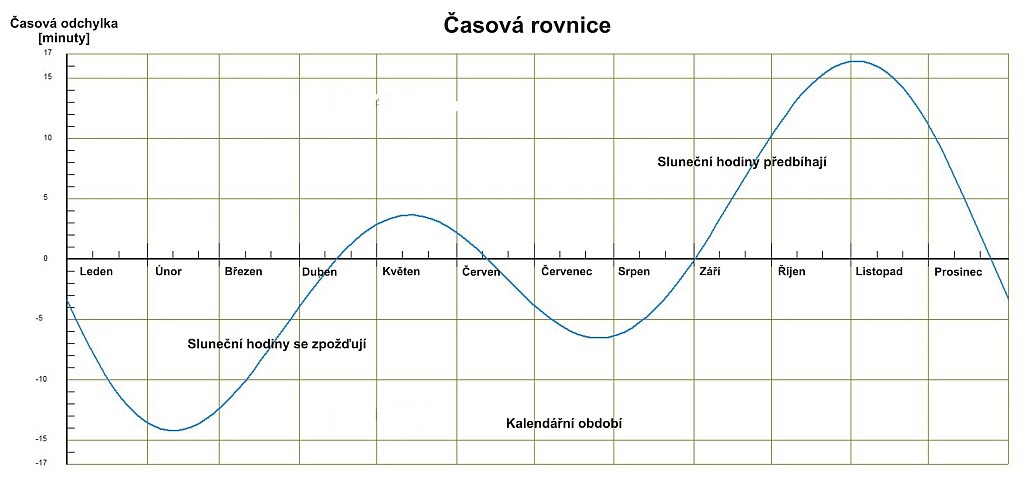
Rozdíl časů pravého Tp (odečtený ze slunečních hodin udávajících čas středoevropského poledníku) a středního Ts (údaj seřízených hodin) se nazývá časovou rovnicí. Pomocí časové rovnice pak můžeme korigovat údaj odečtený ze slunečních hodin Ts = Tp - E a určit čas zpravidla s přesností na 1 minutu.
Na vodorovné ose jsou dny v roce. Na svislé ose jsou časové rozdíly mezi pravým slunečním časem a středním (rovnoměrně plynoucím). Čtyřikrát do roka (15. dubna, 14. června, 31. srpna a 24. prosince) je časová rovnice rovna nule. Tehdy jsou časové údaje slunečních hodin (pokud jsou navrženy aby udávaly čas středoevropského poledníku) s rovnoměrným časem našich hodinek shodné. Kladné hodnoty (15. 4. - 14.6. a 31. 8. - 24. 12.) znamenají, že čas měřený slunečními hodinami předbíhá rovnoměrný čas našich hodinek a záporné hodnoty (14. 6. - 31. 8. a 24. 12. - 15. 4.) naopak, že se údaj slunečních hodin zpožďuje.
V obdobích, kdy je časová rovnice kladná, stín ukáže na hodinovou čáru pro celou hodinu dříve než časové znamení pro shodnou hodinu. Říkáme, že tehdy se sluneční hodiny předbíhají.
Naopak, v obdobích, kdy je časová rovnice záporná, stín ukáže na hodinovou čáru pro celou hodinu později, než časové znamení pro shodnou hodinu. Říkáme, že tehdy se sluneční hodiny zpožďují. Ve dnech, kdy je časová rovnice rovna nule, jsou oba časové údaje shodné.
Jednotlivé okamžiky (východ, pravé sluneční poledne či západ Slunce) nastávají na stanovištích s odlišnou zeměpisnou délkou
od středního poledníku (15°) v různou dobu.
Rozdílu zeměpisné délky 1° odpovídá časový rozdíl 4 minuty, rozdílu 1' odpovídá časový posun o 4 sekundy.
Například v Českém Těšíně na poledníku 18° 37´ (rozdíl proti středoevropskému poledníku 3° 37´) nastávají tyto okamžiky o 14 minut 28 sekund dříve a naopak pro Aš na poledníku 12° 11´ (rozdíl proti středoevropskému poledníku 2° 49´) nastávají tyto okamžiky o 11 minut 16 sekund později.
Protože drtivá většina slunečních hodin udává pravý sluneční čas místního poledníku, je třeba do korekce zahrnout nejen časovou rovnici, ale i zmíněnou odchylku způsobenou odlišnou zeměpisnou délkou stanoviště od středního poledníku. To je dalším důvodem, proč se časový údaj odečtený ze slunečních hodin od údaje našich hodinek liší. Údaj našich hodinek naopak vychází z pásmového času, tj. času odpovídajícím času středního poledníku daného pásma (u nás poledník 15° východně od Greenwiche).
Pokud chceme z časového údaje odečteného na slunečních hodinách určit rytmický čas na jaký jsme zvyklí (čas našich hodinek), musíme
použít korekční křivku nebo tabulku.
Některé hodiny jsou již pro tuto možnost vybaveny.
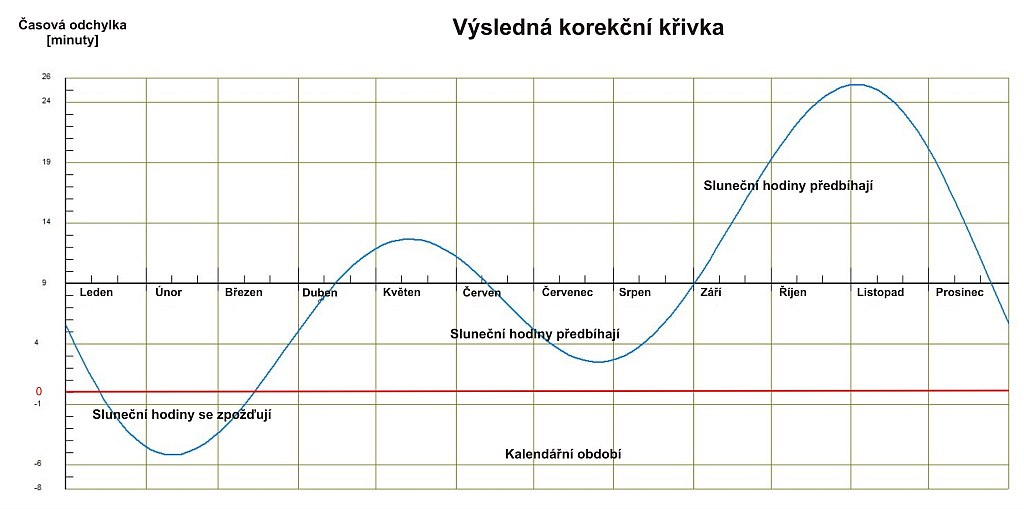
Příklad toho, jak může výsledný korekční graf vypadat, je ukázán pro stanoviště v Ostravě (nám. Republiky). Pro přehlednost je červenou čárou vyznačeno rozhraní, kdy je korekce nulová. Ke shodě časového údaje slunečních hodin na tomto stanovišti s rovnoměrným časem našich hodinek dojde jen dvakrát v roce - zhruba v polovině ledna a března. Po většinu roku na tomto stanovišti údaj odečtený ze slunečních hodin předbíhá údaj na našich hodinkách.
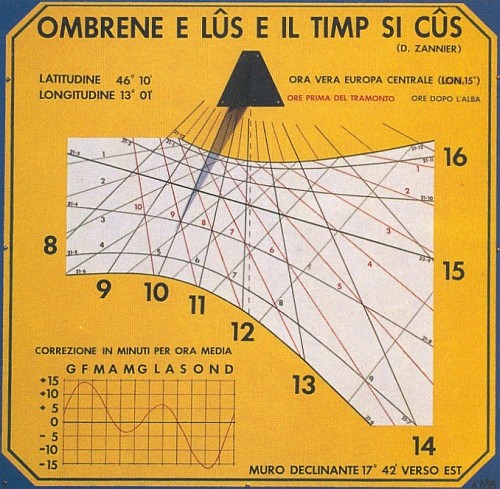
Na číselníku slunečních hodin mohou být korekční údaje uváděny v různé podobě .
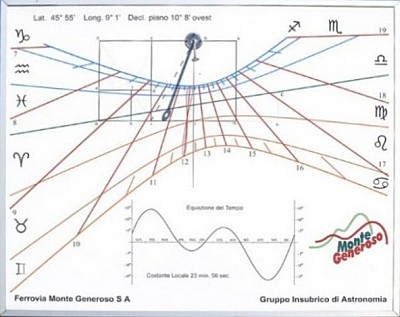

Mohou být vybaveny tabulkou, která může mít zase mnoho forem.



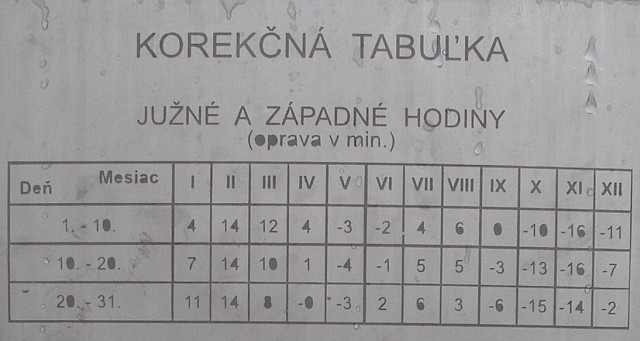
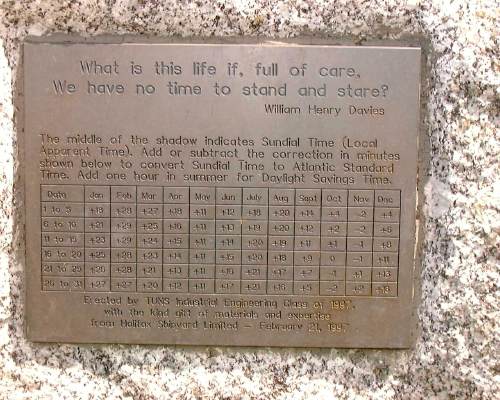
Z tabulky zjistíme kolik minut máme přičíst k času odečtenému ze slunečních hodin nebo od zjištěného časového údaje naopak odečíst.
Jinak se používá následující tabulka.

Korekční údaj je na této tabulce uveden pro čas, kdy hodiny udávají místní poledne pravého slunečního času. Pro jiné doby si musíme hodnotu korekce spočítat.
Drtivá většina hodin na pevných stanovištích u nás pracuje na principu hodinového úhlu. Tento princip si ve stručnosti připomeneme.
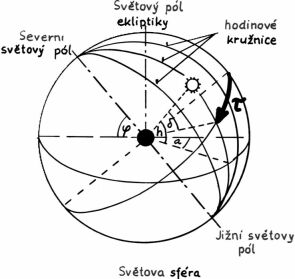
Černý bod uprostřed sféry je naše planeta. K popisu zdánlivého pohybu Slunce se používá různých proměnných: azimut (a), výška Slunce (h), deklinace (d-delta), hodinový úhel (t-tau).
Zeměkoule se otočí kolem své osy přibližně jednou za 24 hodin. Světovou sféru lze pomyslně rozdělit na 24 dílů tzv. hodinovými kružnicemi. Tyto prochází póly. Protože plnému úhlu 360° sluneční dráhy během dne odpovídá 24 hodin, připadá na 1 hodinu úhel 15°.
Je - li stínový ukazatel slunečních hodin rovnoběžný se zemskou osou, pomyslně se Slunce okolo ukazatele otáčí přibližně o 15° za jednu hodinu.
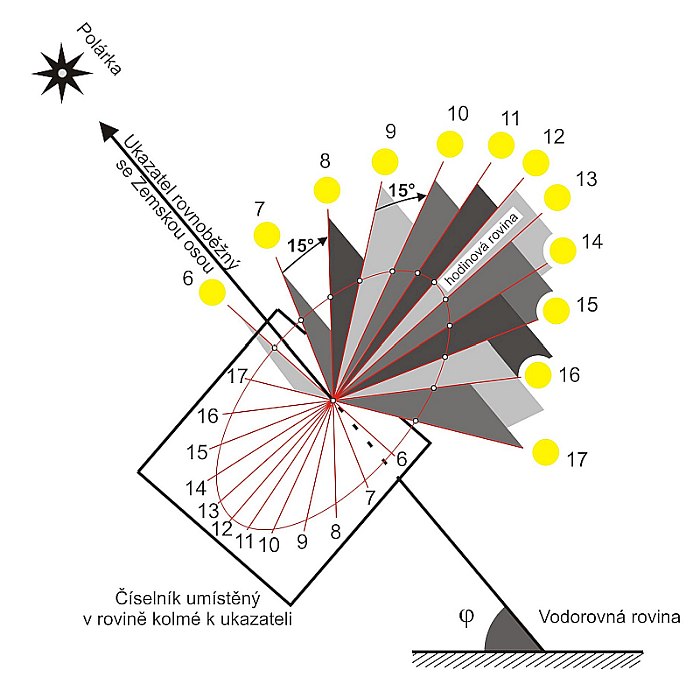
Nejlépe je tento princip patrný na rovníkových hodinách. Svůj název dostaly díky tomu, že číselník je rovnoběžný s rovníkem. Stínový ukazatel, který je rovnoběžný se zemskou osou, je k tomuto číselníku kolmý. Hodinové čáry jsou rozmístěny po uvedených 15°. Princip je patrný z obr. vpravo.
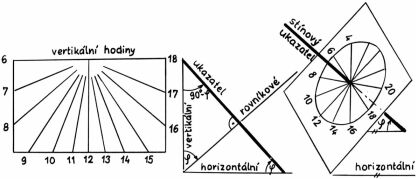
Vzájemné polohy číselníků vodorovných, svislých a rovníkových hodin jsou patrné ze střední části obrázku.
Jiným případem jsou polární hodiny. U těchto jsou hodinové přímky rovnoběžné se zemskou osou a tedy i navzájem. Je - li číselníkem vnitřní plocha válce (polární válcové), jsou na něm rovnoměrně rozmístěny opět po 15°.